무작위 행보
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
무작위 행보는 시작점을 기준으로, 다음 점까지의 거리가 같고, 방향은 임의로 선택되는 경로를 의미한다. 수학적으로는 독립적이고 동일한 분포를 따르는 확률 변수의 합으로 정의되며, 특히 정수 격자에서 각 방향으로 이동할 확률이 동일한 경우 단순 무작위 행보라고 한다. 1차원 또는 2차원에서는 재귀적이지만, 3차원 이상에서는 비재귀적인 성질을 갖는다. 무작위 행보는 중심 극한 정리 및 돈스커 정리에 의해 비너 과정으로 수렴하며, 1차원 단순 무작위 행보는 도박꾼의 파산 문제와 관련이 있다. 다양한 공간과 시간에서 정의될 수 있으며, 자기 상호작용, 상관 관계, 최대 엔트로피 등의 변형된 모델이 존재한다. 물리학, 화학, 금융 경제학 등 다양한 분야에서 현상을 설명하고 모델링하는 데 활용된다.
더 읽어볼만한 페이지
- 무작위성 - 무선 배치
무선 배치는 실험 참가자를 무작위로 그룹에 할당하여 실험군과 대조군 간의 체계적인 차이를 줄이는 방법으로, 연구 결과의 타당성을 높이는 데 기여하며, 무작위 표집과는 다른 개념으로 찰스 샌더스 퍼스, 예르지 네이만, 로널드 A. 피셔 등의 학자들이 그 중요성을 강조했다. - 확률 과정 - 마르코프 연쇄
마르코프 연쇄는 현재 상태가 주어졌을 때 과거와 미래 상태가 독립적인 확률 변수 순서열로, 시간 동질성, 상태 공간 유형, 시간 매개변수 유형에 따라 다양한 유형으로 분류되며 여러 분야에서 활용되는 확률적 모델링 방법이다. - 확률 과정 - 브라운 운동
브라운 운동은 액체나 기체 속 미세 입자가 매질 분자와 충돌하여 불규칙하게 움직이는 현상으로, 아인슈타인과 스몰루호프스키의 이론적 설명과 페랭의 실험적 검증을 통해 원자 존재 입증에 기여했으며, 확산/랑주뱅 방정식으로 모델링되어 다양한 분야에 응용된다. - 물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다. - 물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.
| 무작위 행보 | |
|---|---|
| 확률론 기초 | |
 | |
| 일반 정보 | |
| 영어 | random walk |
| 일본어 | ランダムウォーク (randamu uōku) |
| 한국어 | 무작위 행보 |
| 확률 이론 | |
| 내용 | 확률 공리 결정론 시스템 비결정론 무작위성 |
| 확률 공간 및 사건 | |
| 내용 | 확률공간 표본공간 사건 전체 포괄 사건 근원사건 상호 배타성 결과 한원소 |
| 실험 및 분포 | |
| 내용 | 실험 베르누이 시행 확률분포 베르누이 분포 이항분포 지수 분포 정규분포 파레토 분포 푸아송 분포 |
| 확률 측정 및 변수 | |
| 내용 | 확률 측도 확률변수 베르누이 과정 연속/이산 기댓값 분산 마르코프 연쇄 관측값 무작위 행보 확률과정 |
| 추가 확률 개념 | |
| 내용 | 여사건 결합 확률 주변 확률 조건부 확률 |
| 확률 법칙 및 정리 | |
| 내용 | 독립 조건부 독립 전체 확률의 법칙 큰 수의 법칙 베이즈 정리 불의 부등식 |
| 다이어그램 | |
| 내용 | 벤 다이어그램 트리 다이어그램 |
2. 정의
무작위 행보는 다음 규칙에 의해 생성된 경로이다.
- 시작점이 있다.
- 경로상의 한 점에서 다음 점까지의 거리는 상수이다.
- 경로상의 한 점에서 다음 점으로의 방향은 특정 선호 조건 없이 임의로 선택된다.
때문에, 무작위 행보는 행적이 불규칙하다. 직접적인 일반화로서, 결정 격자(결정 구조의 추상화) 위의 랜덤워크가 정식화되었으며, 중심 극한 정리와 대편차의 성질이 코타니와 스나다에 의해 증명되었다.
2. 1. 수학적 정의
()를 독립이고 동일한 분포를 따르는 값의 확률 변수족이라고 할 때,:
를 ( 차원) 랜덤워크 (random walk, RW)라고 한다.
특히, 이 값을 가지고,
:
(는, 제 성분이 1인 단위 벡터)일 때, ''S''''n''을 ( 차원) 단순 랜덤워크 (simple random walk)라고 한다.
3. 기본적 성질
무작위 행보는 차원에 따라 다른 특징을 보인다. 1차원 또는 2차원 무작위 행보는 재귀성을 가지며, 3차원 이상에서는 비재귀적이다.[62][63] 또한, 무작위 행보는 돈스커 정리에 따라 비너 과정으로 수렴할 수 있다.
3. 1. 재귀성
1차원 또는 2차원의 단순 무작위 행보는 재귀적이며, 3차원 이상의 무작위 행보는 비재귀적이다.[62][63]3. 2. 돈스커의 정리 (Donsker's Theorem)
비너 과정은 1차원에서 무작위 보행의 척도 극한이다. 이는 단계가 매우 작은 무작위 보행이 있다면 비너 과정에 대한 근사가 있다는 것을 의미한다. 더 정확히 말하면, 단계 크기가 ε인 경우, 비너 길이 ''L''을 근사하기 위해 ''L''/ε2 길이의 보행을 해야 한다. 단계 크기가 0으로 (그리고 단계 수가 비례적으로 증가) 향함에 따라, 무작위 보행은 적절한 의미에서 비너 과정으로 수렴한다.무작위 보행이 비너 과정으로 수렴하는 것은 중심 극한 정리와 돈스커 정리에 의해 제어된다. ''t'' = 0에서 알려진 고정 위치에 있는 입자의 경우, 중심 극한 정리는 무작위 보행에서 많은 수의 독립적인 단계를 거친 후, 보행자의 위치가 총 분산의 정규 분포에 따라 분포된다는 것을 알려준다.
:
여기서 ''t''는 무작위 보행 시작 이후 경과된 시간이고, 는 무작위 보행의 한 단계의 크기이며, 는 두 개의 연속적인 단계 사이의 경과된 시간이다.
이는 비너 과정을 제어하는 확산 방정식의 그린 함수에 해당하며, 이는 많은 단계를 거친 후, 무작위 보행이 비너 과정으로 수렴함을 시사한다.
''X''''n'' (''n'' = 0, 1, ...)를 평균 0, 분산 1인 독립적이고 동일한 분포를 갖는 1차원 무작위 보행이라 하고,
:
로 정의하면, 각 ''t'' ≧ 0에 대해 다음이 성립한다.
:
4. 격자 무작위 행보
정규 격자에서의 무작위 행보 모델은 각 단계에서 위치가 특정 확률 분포에 따라 다른 위치로 이동한다. 단순 무작위 행보에서 위치는 격자의 인접한 위치로만 이동할 수 있으며, 격자 경로를 형성한다. 국소 유한 격자에서의 단순 대칭 무작위 행보에서 위치가 각 인접 이웃으로 이동할 확률은 동일하다. 가장 잘 연구된 예는 ''d''차원 정수 격자(때로는 초입방 격자라고 함) 에서의 무작위 행보이다.[3]
상태 공간이 유한 차원으로 제한되면 무작위 행보 모델을 ''단순 경계 대칭 무작위 행보''라고 하며, 전이 확률은 상태의 위치에 따라 달라지는데, 이는 여백 및 모서리 상태에서는 이동이 제한되기 때문이다.[4]
결정 격자(결정 구조의 추상화) 위의 무작위 행보는 직접적인 일반화로 정식화되었으며, 중심 극한 정리와 대편차의 성질은 코타니와 스나다에 의해 증명되었다.
4. 1. 1차원 무작위 행보
1차원 무작위 행보는 0에서 시작하여 각 단계마다 동일한 확률로 +1 또는 -1로 움직이는 것을 말한다. 이는 정수 수직선 위에서 이루어지며, 가장 기본적인 무작위 행보의 예시이다.[6]이러한 움직임은 동전 던지기에 비유할 수 있다. 앞면이 나오면 오른쪽으로 한 단위, 뒷면이 나오면 왼쪽으로 한 단위 움직이는 것이다. 이를 수식으로 표현하면, 독립적인 확률 변수 를 사용하여 각 변수가 1 또는 -1의 값을 50% 확률로 갖도록 설정하고, 및 로 정의할 수 있다. 여기서 수열 은 ''에서의 단순 무작위 행보''라고 불린다.[6]
의 기대치 는 0이다. 즉, 평균적으로는 항상 0에 위치하게 된다. 그러나 표준편차는 에 비례하여 증가한다.[5]
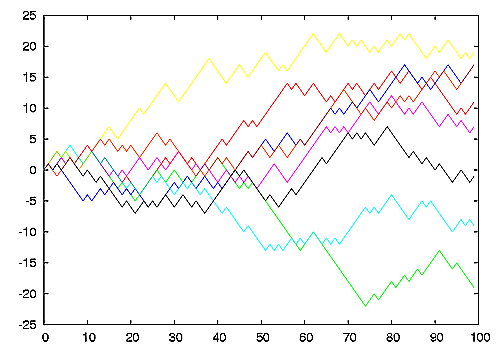
1차원 무작위 행보는 모든 점을 무한히 많이 교차하는 특징을 가지는데, 이를 "레벨 교차 현상", "재귀", 또는 "도박꾼의 파산"이라고도 한다. 도박꾼의 파산 문제는 유한한 돈을 가진 도박꾼이 무한한 돈을 가진 은행을 상대로 공정한 게임을 할 때 결국 돈을 모두 잃게 된다는 것을 의미한다. 도박꾼의 돈은 무작위 행보를 따르며, 결국 0에 도달하여 게임이 종료되기 때문이다.[6]
만약 ''a''와 ''b''가 양의 정수라면, 0에서 시작하는 1차원 단순 무작위 행보가 처음으로 ''b'' 또는 −''a''에 도달할 때까지의 기대되는 단계 수는 ''ab''이다. 이 행보가 −''a'' 전에 ''b''에 도달할 확률은 이며, 이는 단순 무작위 행보가 마팅게일이라는 사실에서 파생될 수 있다.[6]
파스칼의 삼각형을 이용하면, ''n''단계의 서로 다른 행보의 수는 2''n''이며, 각 행보는 동일한 확률로 발생한다. 일 확률은 와 같다.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
중심 극한 정리에 따르면, ''n''이 증가함에 따라 확률은 정규 분포에 접근한다.
4. 2. 고차원 무작위 행보

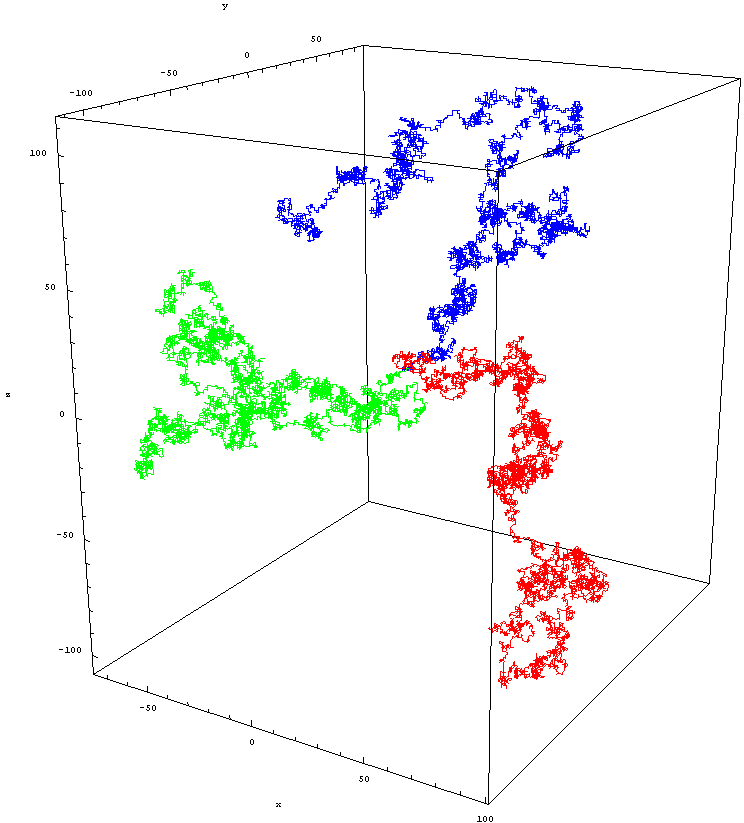
가우스 확률적 보행의 제곱 오차 거리, 즉 2차 속도-왜곡 함수와 관련된 정보율은 다음과 같이 매개변수적으로 주어진다.[26]
:
:
여기서 이다. 따라서, 을 비트 미만의 이진 코드를 사용하여 인코딩하고 미만의 예상 평균 제곱 오차로 복구하는 것은 불가능하다. 반면에, 임의의 에 대해, 이 코드를 사용하여 을 복구할 때 예상 평균 제곱 오차가 이하가 되도록, 개의 고유한 요소로 구성된 이진 코드와 충분히 큰 이 존재한다.
5. 다양한 무작위 행보 모델
인기 있는 무작위 행보 모델은 정규 격자에서 각 단계마다 특정 확률 분포에 따라 위치가 이동하는 방식이다. 단순 무작위 행보에서는 위치가 격자의 인접한 위치로만 이동하여 격자 경로를 형성한다. 국소 유한 격자에서 단순 대칭 무작위 행보는 위치가 각 인접 이웃으로 이동할 확률이 동일하다. 가장 잘 연구된 예는 ''d''차원 정수 격자 (초입방 격자라고도 함) 에서의 무작위 행보이다.[3]
상태 공간이 유한 차원으로 제한되면, 무작위 행보 모델은 ''단순 경계 대칭 무작위 행보''라고 불린다. 이 경우 전이 확률은 상태의 위치에 따라 달라지는데, 여백 및 모서리 상태에서는 이동이 제한되기 때문이다.[4]
순수한 무작위 행보 외에도 더 일반화된 구조를 가진 다양한 확률 과정이 연구되었다. 무작위 행보는 그래프, 정수, 실수선, 평면, 고차원 벡터 공간, 곡면, 고차원 리만 다양체, 군 등 다양한 공간에서 발생할 수 있다. 시간을 무작위로 하여 위치를 정의하는 레비 비행과 브라운 운동과 같은 확산 모델도 있다.
그래프 ''G''에서 루트 ''0''에서 시작하는 길이 ''k''의 무작위 행보는 확률 변수 를 갖는 확률 과정으로, 이고, 는 의 이웃에서 균일하게 무작위로 선택된다. 는 ''v''에서 시작하여 ''w''에서 끝나는 길이 ''k''의 무작위 행보 확률이다. 특히, ''G''가 루트 ''0''을 갖는 그래프인 경우, 는 단계 후 ''0''으로 돌아올 확률이다.
도시가 완벽한 정사각형 격자가 아닌 경우, 특정 교차로에서 사람은 여러 도로 중 하나를 동일한 확률로 선택한다. 이는 그래프에서의 무작위 행보로, 사람은 상당히 완만한 조건에서 거의 확실하게 집에 도달할 수 있다.[44] 이 결과는 전기 네트워크와의 연결을 통해 증명할 수 있으며, 그래프의 과도성 및 재발성 분석에 사용된다.
그래프에서의 무작위 행보는 마르코프 연쇄의 특별한 경우로, ''시간 대칭'' 또는 ''가역성'' 속성을 갖는다. 1980년대부터 그래프 속성과 무작위 행보를 연결하는 연구가 진행되었으며, 등주 부등식, 소볼레프 부등식, 푸앵카레 부등식 등과 관련된다. 랜덤 그래프, 특히 에르되시-레니 모형에서 무작위 보행자의 처음[45]과 마지막 방문 시간[46] 분포 등이 분석되었다.
전이 커널 자체가 무작위인 경우(환경 에 따라) "무작위 환경에서의 무작위 행보"라고 한다. 법칙이 의 무작위성을 포함하면 어닐링된 법칙, 고정되면 퀜칭된 법칙이라고 한다.
모든 경로가 동일한 확률을 갖도록 하는 최대 엔트로피 무작위 행보(MERW)는 더 강력한 국소화 속성을 갖는다.[47]
- 레비 더스트: 우주 공간의 별 분포 모델. 진행 방향은 무작위, 진행 거리 분포는 멱급수로 주어지는 무작위 보행.
5. 1. 자기 상호작용 무작위 행보
복잡한 방식으로 각 단계가 과거에 의존하는 흥미로운 무작위 경로 모델이 많이 있다. 이 모델들은 일반적인 무작위 보행보다 분석적으로 해결하기 더 복잡하다. 그럼에도 불구하고, 무작위 보행자 모델의 동작은 컴퓨터를 사용하여 얻을 수 있다. 예시는 다음과 같다.: 상의 길이 ''n''인 자기 회피 보행은 원점에서 시작하여 에서 인접한 사이트 사이에서만 이동하며, 사이트를 다시 방문하지 않고, 이러한 모든 경로 중에서 균일하게 선택되는 무작위 ''n'' 단계 경로이다. 2차원에서는 자기 트래핑으로 인해 전형적인 자기 회피 보행은 매우 짧으며,[49] 더 높은 차원에서는 모든 경계를 넘어 성장한다.
:이 모델은 (1960년대 이후) 고분자 물리학에서 자주 사용되었다.
: 궤적이 교차하지 않는 무작위 보행. 이론적인 해석은 어렵다. 고분자의 기하학적 구조[65], 해안선 등의 모델 (자기 유사성)로 이용되고 있다.
5. 2. 상관된 무작위 행보 (Correlated random walks)
다음 시간의 이동 방향이 이전 시간의 이동 방향과 상관 관계를 갖는 무작위 행보이다. 이는 동물의 움직임을 모델링하는 데 사용된다.[54][55]5. 3. 최대 엔트로피 무작위 행보 (Maximal entropy random walk)
최대 엔트로피율을 갖도록 선택된 무작위 행보는 훨씬 더 강력한 국소화 특성을 갖는다.[1]6. 응용

무작위 행보는 넓은 범위의 자연 현상을 설명하는데 사용되며, 특히 물리학[27] [28], 화학[29], 재료 과학[30] [31], 생물학[32] [33] [34] 분야에서 두드러진다. 다음은 무작위 행보의 구체적인 응용 분야이다.
- 금융 경제학에서 무작위 행보 가설은 주가 및 기타 요인을 모델링하는 데 사용된다.[35] 실증 연구 결과 이 이론적 모델에서 특히 단기 및 장기 상관 관계에 대한 몇 가지 편차가 발견되었다. 주가 참조.
- 집단 유전학에서 무작위 행보는 유전자 부동의 통계적 특성을 설명한다.
- 물리학에서 무작위 행보는 액체와 기체 속 분자의 무작위 운동과 같은 물리적인 브라운 운동과 확산의 단순화된 모델로 사용된다. (확산 제한 응집 참고). 또한, 양자장론에서도 역할을 한다.
- 반도체 제조에서 무작위 행보는 더 작은 노드에서의 열 처리 효과를 분석하는 데 사용된다. 이는 중요한 제조 단계 동안 도펀트, 결함, 불순물 등의 확산을 이해하는 데 적용된다. 또한, 화학 기상 증착 공정 동안 반응물, 생성물 및 플라즈마의 확산을 연구하는 데 사용된다.
- 수학적 생태학에서 무작위 행보는 개별 동물의 움직임을 설명하고, 확산 과정을 경험적으로 지원하며, 때때로 집단 역학을 모델링하는 데 사용된다.
- 고분자 물리학에서 무작위 행보는 이상적인 사슬을 설명한다. 이는 고분자 연구를 위한 가장 간단한 모델이다.[36]
- 수학의 다른 분야에서 무작위 행보는 라플라스 방정식의 해를 계산하고, 조화 척도를 추정하며, 수학적 분석 및 조합론에서 다양한 구성을 위해 사용된다.
- 컴퓨터 과학에서 무작위 행보는 웹의 크기를 추정하는 데 사용된다.[37]
- 영상 분할에서 무작위 행보는 각 픽셀과 연결할 레이블("객체" 또는 "배경")을 결정하는 데 사용된다.[38] 이 알고리즘은 무작위 보행자 분할 알고리즘이라고 한다.
- 뇌 연구에서 무작위 행보와 강화된 무작위 행보는 뇌 내 뉴런 발화의 캐스케이드를 모델링하는 데 사용된다.
- 시각 과학에서 안구 부유는 무작위 행보처럼 행동하는 경향이 있다.[39] 일부 저자에 따르면, 일반적으로 주시 운동도 무작위 행보로 잘 설명된다.[40]
- 심리학에서 무작위 행보는 결정을 내리는 데 필요한 시간과 특정 결정이 내려질 확률 사이의 관계를 정확하게 설명한다.[41]
- 무작위 행보는 알려지지 않거나 매우 큰 상태 공간에서 샘플링하는 데 사용될 수 있다. (예: 인터넷에서 무작위 페이지 선택)
- 무선 네트워킹에서 무작위 행보는 노드 이동을 모델링하는 데 사용된다.
- 운동성 세균은 편향된 무작위 보행을 한다.[42]
- 물리학에서 무작위 행보는 페르미 추정 방법의 기초가 된다.
- 웹에서 트위터 웹사이트는 누구를 팔로우할지 제안하기 위해 무작위 행보를 사용한다.[43]
- 데이브 바이어와 퍼시 디아코니스는 7번의 셔플로 카드 한 벌을 섞기에 충분하다는 것을 증명했다(자세한 내용은 셔플 참조).
'''레비 더스트'''
: 우주 공간의 별 분포 모델로 생각된 점의 분포. 점이 진행하는 방향을 무작위로 하고, 진행 거리의 분포가 멱급수로 주어지는 무작위 보행.
'''Self-avoiding walk영어'''[64]
: 궤적이 교차하지 않는 무작위 보행. 이론적인 해석은 어렵다. 고분자의 기하학적 구조[65], 해안선 등의 모델 (자기 유사성)로 이용되고 있다.
참조
[1]
논문
The Problem of the Random Walk
[2]
서적
Theory and Applications of Monte Carlo Simulations
https://books.google[...]
IntechOpen
2013
[3]
서적
Random walk in random and nonrandom environments
World Scientific
1990
[4]
간행물
Expected Coverage of Random Walk Mobility Algorithm
[5]
웹사이트
Random Walk-1-Dimensional – from Wolfram MathWorld
http://mathworld.wol[...]
Mathworld.wolfram.com
2000-04-26
[6]
문서
Random walk models in biology
2008
[7]
서적
Spectral geometry of crystal lattices
[8]
논문
Large deviation and the tangent cone at infinity of a crystal lattice
[9]
웹사이트
Pólya's Random Walk Constants
http://mathworld.wol[...]
Mathworld.wolfram.com
2016-11-02
[10]
서적
Probability: Theory and Examples
https://archive.org/[...]
Cambridge University Press
[11]
논문
Pólya's Random Walk Theorem
https://www.jstor.or[...]
2014
[12]
논문
Polya′s Random Walk Theorem Revisited
https://www.jstor.or[...]
2015
[13]
서적
Probability; Combinatorics; Teaching and learning in mathematics
https://archive.org/[...]
MIT Press
1984
[14]
논문
Some intersection properties of random walk paths
1960
[15]
PDF
lec01.pdf
https://ocw.mit.edu/[...]
2024-08
[16]
논문
MATHEMATICS: Taking the Measure of the Wildest Dance on Earth
[17]
문서
Chapter 2 DIFFUSION
http://engineering.d[...]
dartmouth.edu
[18]
웹사이트
Diffusion equation for the random walk
http://nebula.physic[...]
physics.uakron.edu
2015-04-21
[19]
서적
Advances in Chemical Physics
[20]
서적
Optical Spectroscopy of Glasses
[21]
논문
Density of states on fractals: " fractons "
https://hal.archives[...]
[22]
논문
Random walks on fractal structures and percolation clusters
https://hal.archives[...]
[23]
논문
Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen
[23]
서적
Diffusion-Limited Reactions
https://books.google[...]
Elsevier
1985-03-01
[24]
논문
Random Dispersal in Theoretical Populations
[25]
논문
Studies in Statistical Ecology: I. Spatial Pattern
[26]
논문
Information rates of Wiener processes
[27]
서적
The Fokker–Planck Equation
Springer, Berlin
1984
[28]
서적
Scaling Concepts in Polymer Physics
Cornell University Press, Ithaca and London
1979
[29]
서적
Stochastic Processes in Physics and Chemistry
North-Holland, Amsterdam
1992
[30]
서적
Aspects and Applications of the Random Walk
North-Holland Publishing Co., Amsterdam
[31]
서적
The Theory of Polymer Dynamics
Clarendon Press, Oxford
1986
[32]
서적
Stochastic Models in Biology
Academic Press, New York
1974
[33]
서적
A Guide to First-Passage Process
Cambridge University Press, Cambridge, UK
2001
[34]
서적
Renewal Theory
Methuen, London
1962
[35]
문서
Forecasting Corporate Revenue and Profit: Time-Series Models versus Management and Analysts
1984
[36]
서적
Soft condensed matter
https://archive.org/[...]
Oxford Univ. Pr.
2004
[37]
간행물
Random sampling from a search engine's index
Association for Computing Machinery (ACM)
[38]
간행물
Random walks for image segmentation
http://cns-web.bu.ed[...]
2016-11-02
[39]
간행물
The unsteady eye: An information-processing stage, not a bug
[40]
간행물
An integrated model of fixational eye movements and microsaccades
[41]
간행물
An exemplar-based random walk model of speeded classification
http://oz.ss.uci.edu[...]
[42]
간행물
Random walk models in biology
2008-08-06
[43]
문서
WTF: The who-to-follow system at Twitter
http://dl.acm.org/ci[...]
Proceedings of the 22nd international conference on World Wide Web
[44]
간행물
Recurrent Graphs where Two Independent Random Walks Collide Finitely Often
https://projecteucli[...]
2004
[45]
간행물
The distribution of first hitting times of randomwalks on Erdős–Rényi networks
[46]
간행물
The distribution of path lengths of self avoiding walks on Erdős–Rényi networks
[47]
간행물
Localization of the Maximal Entropy Random Walk
[48]
서적
The Self-Avoiding Walk
Birkhäuser Boston
1996
[49]
간행물
An average self-avoiding random walk on the square lattice lasts 71 steps
[50]
서적
Intersection of random walks
Birkhäuser Boston
1996
[51]
문서
Conformally Invariant Processes in the Plane
http://www.math.corn[...]
[52]
간행물
A survey of random processes with reinforcement
http://www.emis.de/j[...]
[53]
간행물
Multi-agent random walks for local clustering on graphs
http://www.kyb.mpg.d[...]
IEEE 10th International Conference on Data Mining (ICDM)
2012-04-15
[54]
간행물
Spatial analysis of animals' movements using a correlated random walk model
[55]
간행물
Analyzing insect movement as a correlated random walk
[56]
웹사이트
ウィーナー過程
http://www.findai.co[...]
フィナンシャル・アーティスト・アカデミー株式会社
[57]
웹사이트
Log normal distribution
http://www.ntrand.co[...]
ニューメリカルテクノロジーズ株式会社
[58]
간행물
Spectral geometry of crystal lattices
[59]
간행물
Large deviation and the tangent cone at infinity of a crystal lattice
[60]
문서
ランダムウォークに関する話題から ―逆正弦法則について―
http://www.nara-wu.a[...]
[61]
문서
“つき”の数理-逆正弦法則について
http://elis.sigmath.[...]
大阪大学基礎工学研究科会田研究室
[62]
문서
ランダムウォーク
http://user.numazu-c[...]
[63]
문서
電気回路とランダム・ウォーク
http://www7b.biglobe[...]
確率統計委員会
2002-03-17
[64]
웹사이트
確率モデルを用いたフラクタル図形の作成に関する実験手引書
https://hdl.handle.n[...]
北海道大学
2020-05-18
[65]
문서
ランダムウォークと統計力学
http://www.ice.gunma[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com